Jasmin Patry
Sucker Punch Productions
Lighting, Atmosphere, and Tonemapping
in
Real-Time Samurai Cinema
© 2021 Sony Interactive Entertainment LLC. Ghost of Tsushima is a trademark of Sony Interactive Entertainment LLC.

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course


Introduction
- Sucker Punch is a part of PlayStation Studios (formerly Sony Interactive Entertainment Worldwide Studios)
- Peak size: 160 people (including 25 QA)
- Previous games include:
- Sly Cooper (1, 2, & 3)
- Infamous (1, 2, Festival of Blood, Second Son, First Light)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course





Introduction
- Ghost of Tsushima released in July 2020 for the PlayStation 4
-
Legends multiplayer expansion released in October 2020
- Also added 60 FPS support for PS5

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course









Introduction | Other Talks

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course





Samurai Landscapes: Building and Rendering Tsushima Island on PS4
Matthew Pohlmann
Samurai Shading in Ghost of Tsushima
Jasmin Patry
Zen of Streaming: Building and Loading Ghost of Tsushima
Adrian Bentley

Procedural Grass in Ghost of Tsushima
Eric Wohllaib

Blowing from the West: Simulating Wind in Ghost of Tsushima
Bill Rockenbeck
Introduction | Goals
- Transport players to 1274 Japan
- Huge open world
- Beautiful, living, breathing
- Continuous time of day with dynamic weather
- Huge open world
- Recreate the style of classic samurai cinema
- “Kurosawa Mode”
- Dramatic lighting, wind, clouds, haze, and fog

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Introduction | Lighting
- Art direction called for “stylized realism”
- Lighting models are physically based
- Materials authored with physically plausible values, some photogrammetry
- Indirect lighting computed at runtime from dynamic sky and local light transfer data
- Physically based sky model, used for sky, clouds, haze, and fog particles
- Rendered in HDR and tonemapped with custom techniques
- Lighting can deviate from physical correctness
- Artists can globally adjust to achieve desired look

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Introduction | Overview
- Indirect lighting
- Diffuse
- Specular
- Atmospheric volumetric lighting
- Skies & clouds
- Haze
- Particles
- Tonemapping
- Local tonemapping operator
- Custom tonemapping color space and white balance
- Purkinje shift (low-light vision simulation)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course


Indirect Lighting| Diffuse
-
Infamous: Second Son used static degree 2 SH irradiance probes in tetrahedral meshes
- See Adrian Bentley's GDC 2014 Talk, “Engine Postmortem of inFAMOUS: Second Son”

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




Indirect Lighting| Diffuse

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course





Indirect Lighting| Diffuse
- Tsushima’s size and dynamic time of day and weather required a new approach
- Regular grid of quadratic SH probes
- 16x16x3 per 200m square tile, 20x80 tiles

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Diffuse

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Diffuse
- Tetrahedral meshes used in for more complex cases
- Towns, villages, farmsteads, castles, etc.
- Streamed in with location
- Overrides regular grid, blends at interface

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




Indirect Lighting| Diffuse
- Tetrahedral meshes used in “locations”
- Towns, villages, castles, etc.
- Streamed in with location
- Overrides regular grid, blends at interface

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




Indirect Lighting| Diffuse
- Tetrahedral meshes used in “locations”
- Towns, villages, castles, etc.
- Streamed in with location
- Overrides regular grid, blends at interface

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course





Indirect Lighting| Diffuse
- Tetrahedral meshes used in “locations”
- Towns, villages, castles, etc.
- Streamed in with location
- Overrides regular grid, blends at interface

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course





Indirect Lighting| Diffuse
- Tetrahedral meshes used in “locations”
- Towns, villages, castles, etc.
- Streamed in with location
- Overrides regular grid, blends at interface

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course





Indirect Lighting| Diffuse
Runtime Relighting
- Need to update our irradiance probes at runtime
- Offline, capture:
- Irradiance

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Diffuse
Runtime Relighting
- Need to update our irradiance probes at runtime
- Offline, capture:
Irradiance- Sky visibility encoded in degree 2 SH (mono)
- At runtime:
- Project sky to SH
- Multiply sky SH by sky visibility
- Convolve with Lambertian cosine lobe

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Diffuse
Bounced Sky Light
- This works, but gives direct sky lighting only
- No bounced light
- Full transfer matrix?
- Too much memory (9X)
- Takes too long to capture
- Approximate by assuming that sky light is ~constant over hemisphere
- Light the world with a uniform white sky
- Capture “bounced sky visibility”
- Multiply by average sky color (from 0th SH band)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Sky Visibility = 1 Everywhere

Sky Visibility

Bounced Sky Visibility

Sky Visibility = 1 Everywhere

Direct Sky Visibility Only

Direct + Bounced Sky Visibility

Indirect Lighting| Diffuse
Adding Sun/Moon Bounce
- Bouncing sky light by itself not sufficient
- Can we use the bounced sky visibility data somehow?
- Idea: consider a fixed set of of bounce directions
- (bounce directions SH) \(\times\)
(bounced sky visibility SH) \(\times\)
(sun/moon irradiance) - Assumes that the cosine-weighted average sky visibility of the surfaces is a good estimate of shadowing
- Close enough for our purposes
- (bounce directions SH) \(\times\)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Diffuse
Adding Sun/Moon Bounce
- Reflect light in imaginary ground and wall
- Project \(-\mathbf{\hat{r}}_g\) and \(-\mathbf{\hat{r}}_w\) to SH; window to avoid negative lobes
- Scale by RGB light intensity (modulated by dynamic cloud shadow)
- Multiply by bounced sky SH and add to previous result

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




No Sun Bounce

With Sun Bounce

Sky Visibility = 1 Everywhere

Sky Visibility

Bounced Sky Visibility

Sky Visibility = 1 Everywhere

Direct Sky Visibility Only

Direct + Bounced Sky Visibility

Direct + Bounced Sky Visibility + Sun Bounce

Indirect Lighting| Diffuse
Directionality Boost
- Degree 2 SH is relatively low frequency
- Indirect lighting looked flat in many areas
- Lerp towards delta in direction of linear SH maximum
- Inexpensive to compute
- Separately computed for direct and bounced portions
- Used 25% boost in all weather states

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



No Directionality Boost

With Directionality Boost

Indirect Lighting| Diffuse
Deringing
- No guarantee that final irradiance will be positive everywhere
- Apply fixed extra deringing to sky visibility?
- Reduces directionality and fidelity
- Instead dering sky luminance and final irradiance at runtime
- Peter-Pike Sloan, “Deringing Spherical Harmonics”, SIGGRAPH Asia 2017
- One Newton step sufficient to find the minimum
- Used a depth 3 binary search tree computed on CPU

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Old Windowing Function (Stupid Spherical Harmonics Tricks)
New Windowing Function
No Deringing

With Deringing

Indirect Lighting| Diffuse
Performance (Base PS4)
- Sky luminance \(\Rightarrow\) SH: 60 μs (including deringing)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



| Operation | Tetrahedral Mesh (~5000 probes) | Grid Update (73 tiles) |
|---|---|---|
| Full Update (baseline) | 60 μs | 123 μs |
| Direct only (no bounce) | 30 μs (-50%) | 110 μs (-11%) |
| Without Deringing | 53 μs (-12%) | 120 μs (-2%) |
| Without Dir. Boost | 60 μs (no change) | 123 μs (no change) |
Bonus Slide
Indirect Lighting| Diffuse
Light Leaking
- In Infamous, worked around light leaking issues
- Few interiors, thick walls
- Lots of interiors and thin walls in Ghost
- Tried augmenting probes with:
- Cone occlusion
- Occlusion planes
- Occlusion maps
- None of these solved all our problems

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Diffuse
Light Leaking Solution
- Classify tetrahedral mesh probes as interior or exterior
- Assign surfaces a 0-1 interior mask \(w_\textrm{interior}\)
- Geometry property or shader parameter
- Vertex paint
- Deferred decal
- Calculate barycentrics as normal, then multiply by weight:
- \(w_\textrm{interior}\) for interior probes
- \(1 - w_\textrm{interior}\) for exterior probes
- Renormalize barycentrics (use original if all 0)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without Interior Mask

Without Interior Mask

Interior Mask Applied

Interior Mask Applied


Interior Mask

Without Interior Mask

Interior Mask Applied

Indirect Lighting| Diffuse
Limitations
- Baked data is completely static
- Objects that could move or be destroyed usually omitted from the bakes
- Bounced light assumption (shadowing \(\approx\) sky visibility) is often wrong
- Bounced light either too strong or too dim
- No indirect light from local lights

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Bonus Slide
Indirect Lighting| Specular
- Seattle in Infamous used 230 static reflection probes
- Already pushing memory limits
- Tsushima used 235
- Extra data required for relighting
- Streamed on demand
- Per-biome default probes
- Instanced interior probes
- Added support for nested probes
- Up to 128 relit probes at a time

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
- Offline captured data:
- Albedo cube map (BC1 format)
- Normal + Depth cube map (BC6H format)
- RG: Octahedral normal encoding
- B: Depth (hyperbolic)
- All cube maps 256x256x6

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course






Indirect Lighting| Specular
Reflection Probe Relighting
- Performed round-robin in async compute (one per frame)
- Shadowed with far shadow map atlas
- Per-tile shadow map, 128x128 texels
- Single SH sample for indirect lighting
- Also used as for reflection probe luminance for normalization
- Prefiltered using filtered importance sampling
- Compressed to BC6H using GPURealTimeBC6H
- Reduced memory footprint and improved sampling performance

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Cube Map Shadow Tracing
- Far shadow maps insufficient for shadowing interiors
- Combination of low shadow resolution and LOD
- Insight: depth cube maps have lots of occlusion information
- When relighting each cube map texel:
- Find intersection of directional light ray
with cube map volume - Sample depth at intersection
- Sky depth \(\Rightarrow\) unoccluded
- Used 4x4 PCF
- Find intersection of directional light ray

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Cube Map Shadow Tracing
- Fairly crude, but cheap and effective

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without Cube Map Shadow Tracing

With Cube Map Shadow Tracing

Indirect Lighting| Specular
Horizon Occlusion
- Account for occlusion of underlying geometry on reflection cone caused by tilt of normal-mapped normal \(\mathbf{\hat{n}}_\mathrm{m}\) relative to vertex normal \(\mathbf{\hat{n}}_\mathrm{v}\)
- Fast, approximate, plausible results
- For GGX roughness \(\alpha\), the cone half-
angle \(\theta_{c}\) containing the fraction \(u_\mathrm{e}\) of the
energy is given by

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Horizon Occlusion

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Horizon Occlusion

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Horizon Occlusion

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Horizon Occlusion

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Indirect Lighting| Specular
Horizon Occlusion

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without Indirect Specular Horizon Occlusion

With Indirect Specular Horizon Occlusion

Indirect Lighting| Specular

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



float SpecularHorizonOcclusion(
float3 normalReflect, float3 normal, float3 normalVtx, float alpha)
{
float radSpecCone = RadHalfConeAngleFromGgxAlpha(alpha);
radSpecCone = max(radSpecCone, 0.4);
float3 normalPlane = normalize(cross(normalReflect, normalVtx));
float3 normalProj = normalize(normal - dot(normalPlane, normal) * normalPlane);
float radNormalProj = RadACosFast01(saturate(dot(normalProj, normalVtx)));
float radReflect = RadACosFast(dot(normalReflect, normalVtx));
float radHorizonOcc = min(radSpecCone + radReflect - pi * 0.5, 2.0 * radNormalProj);
float uRadHorizonOcc = saturate(radHorizonOcc / (2.0 * radSpecCone));
float uSpecularOcc = GSquare(uRadHorizonOcc) * (2.0 - GSquare(uRadHorizonOcc));
uSpecularOcc *= 0.95;
return saturate(1.0 - uSpecularOcc);
}
Bonus Slide
Indirect Lighting| Specular
Roughness Parallax Compensation
- Parallax correction within reflection probe volumes
distorts apparent roughness - For current eye position \(d_e\) units from sample location,
with cube map capture location \(d_c\) units away,
we have
- So, when sampling the cube map we use

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without Parallax Compensation

Without Parallax Compensation


With Parallax Compensation


Indirect Lighting| Specular
Performance (Base PS4)
- Shadow tracing accounts for ~16% of the relighting cost
- Horizon occlusion accounts for ~3% of deferred lighting cost
- Roughness parallax compensation has negligible cost

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



| Step | Time (μs) |
|---|---|
| Relight reflection probe |
347
|
| Generate mipmaps | 37 |
| Convolve with GGX NDF | 250 |
| Compress to BC6H | 60 |
| Total | 700 |
Bonus Slide
Atmospheric Lighting

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course


Atmospheric Lighting
- All of our atmospheric lighting used pre-calculated 3D LUTs
- Rayleigh and Mie inscattering (divided by phase functions)
indexed by altitude, sun/moon polar angle, and
view polar angle - Multiple scattering
- Bruneton08, Elek09, Yusov13
- Analytic Earth shadow term
- Rayleigh and Mie inscattering (divided by phase functions)
- Precision issues when using this LUT to light clouds, haze, and fog
- Extended with parallel LUT to store radiance divided by phase function
- I.e., average irradiance

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting
- Apply shadowing to the Mie irradiance, and ambient occlusion to the Rayleigh irradiance
- Mie phase function is strongly forward-scattering
- Rayleigh scattering is closer to uniform
- Haze uses average sky visibility for AO
- Plus rain shadow map for interiors
- Clouds render to a paraboloid texture
- Rgb11f
- Red: Mie
- Green: Rayleigh
- Blue: Transmittance

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course






Without Multiple Scattering For Clouds, Haze, and Particles

With Multiple Scattering For Clouds, Haze, and Particles

Atmospheric Lighting
- Each frame, resample 3D LUTs into 2D for current sun and
moon angles - Upsample using cubic filtering to avoid aliasing at sunrise
and sunset - Makes later lookups cheaper

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting
Custom Rayleigh Color Space
- The atmosphere drives most of our world lighting, so
getting Rayleigh scattering right was important - A blog post by Christian Schüler gave us the idea to try to find a color space that gave results closer to spectral rendering
- Minimized the error in Rayleigh transmittance in two steps:
- Choosing three wavelengths (LMS) for our primaries with point-sampled Rayleigh coefficients
- Refined the Rayleigh coefficients for the color space chosen in step 1.

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



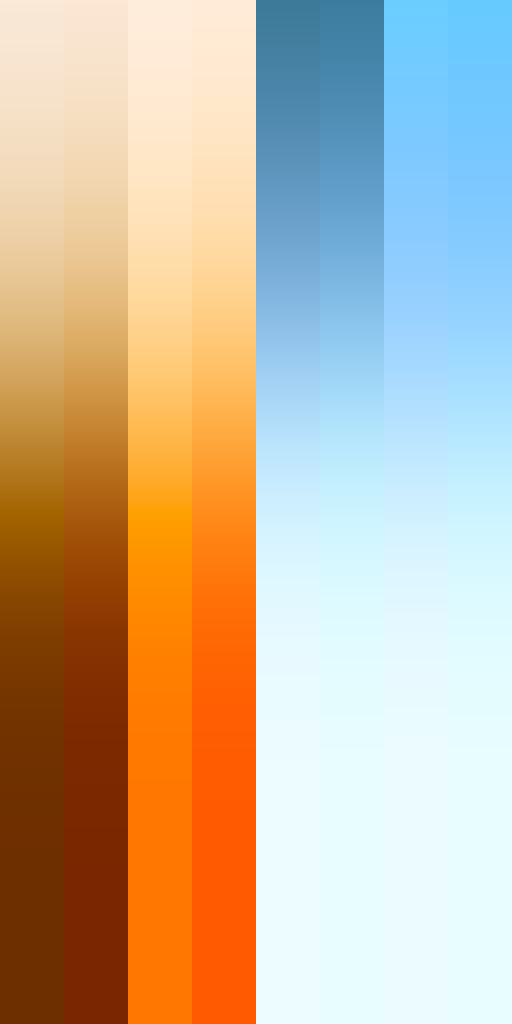
Spectral vs Rec.709 with Bruneton08 Coefficients
Spectral
Rec.709
Spectral
Rec.709
Spectral
Rec.709
Spectral
Rec.709
Transmittance
Outscattering
Hue
Hue
Absolute
Absolute
Transmittance
Outscattering
Hue
Hue
Absolute
Absolute
Spectral
LMS
Spectral
LMS
Spectral
LMS
Spectral
LMS
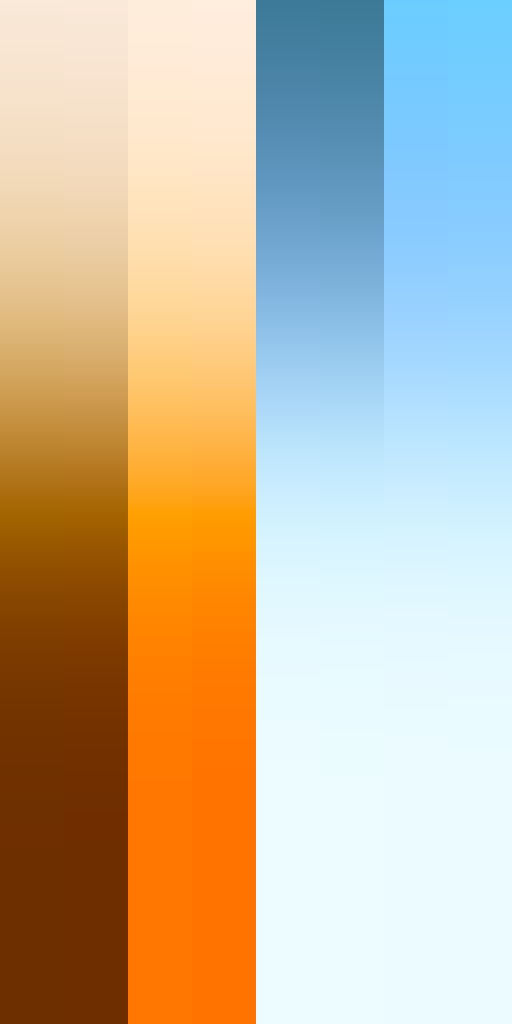
Spectral vs LMS Color Space
Rec.709 Color Space

New LMS Color Space

Atmospheric Lighting
Custom LMS Rayleigh Color Space
White point (D65):

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Rayleigh scattering coefficients:
Primaries:
CIE 1931 Chromaticity Diagram
Atmospheric Lighting| Clouds
- Schneider 2015, Hillaire 2016
- Clouds rendered to 768x768 paraboloid texture
- Three textures:
- Two for scrolling & lerping
- One for rendering (timesliced over 60 frames)
- Three textures:
- Antialiasing for cloud density:
- Calculate derivatives of:
- Radial cloud position with radial texture coordinate
- Angular cloud position with angular texture coordinate
- Reduce cloud density when derivative is high
- Calculate derivatives of:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



No Cloud Density AA

With Cloud Density AA

Atmospheric Lighting| Clouds
- For Mie scattering, use Henyey-Greenstein phase function
- Asymmetry \(g\) depends on how “deep” we are in cloud
- Estimate using product of:
- Transmittance to light
- Transmittance of current raymarch segment
- 0 \(\Rightarrow\) Backscattering (\(g\approx -0.15\))
- 1 \(\Rightarrow\) Forward Scattering (\(g\approx 0.85\))
- Gives “silver lining” for backlit clouds, dark edges for front-lit clouds
- Scale backscattering by ~2.16 to account for multiple scattering
- Based on simulation with albedo of 0.9

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Only Forward Scattering

Only Backscattering

Combined Forward and Backscattering

Backlit “Silver Lining”

Atmospheric Lighting| Volumetric Haze
- Wronski 2014, Drobot 2017a
- Froxel grid, 128 W x 64 H x 64 D
- Covers entire depth range (10 cm to 100 km)
- Exponential depth distribution: \(\Delta z_{i+1} = 1.2 \Delta z_i\)
- Uses only analytic and integrable density functions
- Exponential height falloff: \(d(z) = d_e e^{\frac{-z}{k_e}}\)
- Sigmoidal height falloff:
- Local variation added with particles

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting| Volumetric Haze
- Single compute dispatch populates froxel grid
- Integrate inscattering front to back with quad swizzling using 4x4x4 threadgroups (Drobot 2017a)
- Temporal filtering:
- Shadow and ambient fraction (RG16f)
- Local lighting (RGB11f)
- Skip lighting of occluded froxels
- Still compute shadow and ambient fraction to reduce reprojection errors
- Async compute (~0.5 ms on base PS4)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting| Volumetric Haze
Local Lighting
- Tiled light culling compute shader also outputs lights for haze
- Light divergence between threads in haze compute shader
hurts performance - Using flat bit arrays (Drobot 2017b) for haze lighting was a big speedup
- For forward-shaded materials, faster to use sorted light indices

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting| Volumetric Haze
Anti-Aliasing
- Froxel volume has very low resolution but covers entire view frustum (10 cm to 100 km)
- Using traditional approach results in bad aliasing at horizon and with thin haze layers (density aliasing)
- Solve by storing inscattered radiance divided by opacity
- Re-apply opacity per-pixel when compositing into scene

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without Density AA

With Density AA

Atmospheric Lighting| Volumetric Haze AA
- Why does this work?
- First, assume that scattering \(\sigma_s(x)\) and extinction \(\sigma_e(x)\) are proportional, where \(c\) is the albedo:
- Start with the volume rendering equation for the inscattered radiance over distance \(d\):

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- \(L_i(x)\) is the integral over the sphere of the incoming radiance times the phase function.
Atmospheric Lighting| Volumetric Haze AA
- Substitute for \(\sigma_s(x)\):
- Now assume that \(L_i(x)\) is relatively constant. Then

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting| Volumetric Haze AA
- Let \(\overline{L}_i(d)\) be the average of \(L_i(x)\) over \([0, d]\):
- This integral simplifies to:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting| Volumetric Haze AA
- The term in square brackets is just the opacity \(\alpha(d)\):
- So, if we divide the inscattering \(L(d)\) by \(\alpha(d)\), we get:
- Therefore we can expect that \(L/\alpha\) is a smoother function than \(L\).

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Atmospheric Lighting| Volumetric Haze AA
More Anti-Aliasing
- Use tricubic B-spline filtering to smooth and denoise
- Relatively inexpensive on an Rgb11f buffer
- Less than 50 us more than trilinear on PS4 Pro
- See this Desmos graph (https://bit.ly/3wZ3aIs)
for fast and accurate approximations of the
weighting functions
- Relatively inexpensive on an Rgb11f buffer

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Trilinear Filtering


Bicubic Filtering


Tricubic Filtering


Trilinear Filtering

Bicubic Filtering

Tricubic Filtering

Atmospheric Lighting| Volumetric Haze AA
Performance

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Bonus Slide
| Filter | Base PS4 (μs) (1080p) |
PS4 Pro (μs) (1800cb) |
|---|---|---|
| Trilinear |
363
|
430 |
| Bicubic |
430
|
443
|
| Tricubic |
667
|
483
|
Atmospheric Lighting| Particle Lighting
- Optional “haze lighting” mode for particles
- In volumetric haze shader we also store \(L_i(x)\)
- Sampled from LUTs, with phase functions, shadowing, and sky visibility fraction applied
- Plus local light contribution
- Applied in particle shader by sampling froxel volume and multiplying \(L_i(x)\) times opacity
- Sample using bicubic filtering when opacity exceeds threshold.

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Particle Haze Lighting Off

Particle Haze Lighting On

Atmospheric Lighting| Particle Lighting
Multiple Scattering Approximation
- High-opacity particles are too dark when lit from the front
- Haze uses predominantly forward (Mie) scattering
- Inexpensive, approximate compensation:
- On CPU, calculate ratio of a back-scattering phase function to haze Mie phase function for \(\mathbf{\hat{v}} = \mathbf{\hat{l}}\) and \(\mathbf{\hat{v}} = -\mathbf{\hat{l}}\)
- In shader, lerp between these two values based on \(\mathbf{\hat{v}}\cdot\mathbf{\hat{l}}\) to get a multi-scattering scale factor \(r_\mathbf{MS}\)
- Lerp from 1 to \(r_\mathbf{MS}\) based on opacity, scale light
- In practice, strength of effect was reduced for back scattering
- Too bright when lacking Mie color contribution

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without Multi-Scattering Approximation

With Multi-Scattering Approximation

Tonemapping

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course


Tonemapping| Exposure
- In the Infamous games, we struggled to maintain physically plausible diffuse albedo values
- Exposure \(\Leftrightarrow\) Albedo feedback loop
- Resulted in albedo values that were too dark
- Created a diffuse color reference chart

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




Tonemapping| Exposure
- In the Infamous games, we struggled to maintain physically plausible diffuse albedo values
- Exposure \(\Leftrightarrow\) Albedo feedback loop
- Resulted in albedo values that were too dark
- Created a diffuse color reference chart
- Switched to a primarily illuminance-based exposure system
- Use luminance only if highlight luminance exceeds threshold
- E.g. Fire particles, bright specular highlights
- Use luminance only if highlight luminance exceeds threshold

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping
Dealing with Dynamic Range
- Dim interior lighting
- Large variation between interior and exterior luminance
- Maintain visibility while avoiding “blow-outs”
- Skies drove most of our lighting
- Brighter than environment
- Wanted to avoid losing color
- See Bart Wronski's blog post for a discussion of this problem

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping
Dealing with Dynamic Range
- In photography and cinematography:
- Graduated filters
- Special lighting rigs, bounce cards
- Dodging & burning
- Digital shadow/highlight adjustment
- HDR photography using multiple exposures
- Human visual system capable of perceiving a very wide dynamic range
- Bilateral filter can be used to maintain image detail while reducing overall contrast

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Original Image

50% Contrast

50% Contrast Using Bilateral Filter

Tonemapping| Bilateral Grid
- Naïve bilateral filters are expensive
- The Bilateral Grid algorithm (Chen et al., 2007) allows efficient computation
- Allows aggressive downsampling
- We used 64 W x 32 H x 64 D (log luminance)
- Naturally fits alongside luminance histogram generation
- Overhead was ~250 us on PS4 at 1080p
- Allows aggressive downsampling

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Bilateral Grid
- Algorithm:
- Populate grid with homogeneous log-luminance values \((w_iV_i, w_i)\)
- Initial weight for each sample based on linear Z weights
- Each sample contributes to two nearest Z slices
- Weighting in X & Y not necessary due to blurring
- Apply Gaussian blur to grid
- Wide blur in X & Y, smaller in Z (or can omit)
- Bilaterally filtered value for a pixel obtained by trilinearly sampling grid and normalizing result

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Bilateral Grid
Detail-Preserving Contrast Adjustment

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- \(I_i\): Input image log luminance
- \(I_o\): Output log luminance
- \(B\): Bilaterally filtered log luminance
- \(M\): Midpoint log luminance
- \(c\): Contrast scale
- \(d\): Detail strength
Tonemapping| Bilateral Grid
Ringing and Haloing Artifacts
- Bilaterally blurring smooth gradients can result in ringing
- E.g., clouds, filtered shadows, specular highlights
- Can be reduced with larger luminance buckets (or wider Z blur)
- Tends to increase halos

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




Tonemapping| Bilateral Grid

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Simulated Ringing Scenario
\(I_i\)
\(I_i\) (input)
\(B\) (bilateral blur)
\(I_o\) (output)
Tonemapping| Bilateral Grid
Eliminating Ringing Artifacts
- Blend between bilateral filter and very wide 2D Gaussian
- We used 40% bilateral, 60% 2D Gaussian
- 2D Gaussian blur must be wide enough to avoid noticeable haloing
- We used a radius 13 Gaussian blur on 64x32 image
- Upsampled to 256x128 using bicubic B-spline filtering
- Avoids bilinear artifacts
- Adds extra blur

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Bilateral Grid

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



\(I_i\)
\(I_i\)
\(B\)
\(I_o\)
Eliminating Ringing Artifacts
50% Contrast Using Bilateral Filter

40% Bilateral Blur + 60% Wide Gaussian Blur

Original Image

Typical In-Game Settings (75% High Contrast, 100% Low Contrast)

50% Detail Strength Boost

Tonemapping| Color Space
- Per-channel tonemapping in the rendering color space clips saturated colors to cyan, magenta, and yellow
- Here we’re just applying the per-channel “Reinhard” operator:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- Color scaled so no component exceeds 1.0
Rec.709 Per-Channel Tonemapping

Tonemapping| Color Space
- One solution: desaturate, tonemap, invert desaturation

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



CUT
Desaturate/Resaturate Tonemap

CUT
Tonemapping| Color Space
- Preserves hue and luminance
- Equivalent to transforming to an expanded gamut
- Color space quickly gets weird, however
- Results aren’t perceptually pleasing
- Choose another color space?
- Tried several: ACES AP0, ACES AP1, Rec.2020, DCI-P3
- ACES AP1 was the best of these, but still bent reds too much towards yellow
- Adjusted red primary x coordinate (0.713 \(\Rightarrow\) 0.75)
- Reduced shift to yellow at sunset without desaturating yellows too much

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



CUT
Tonemapping| Color Space
- Choose another color space?
- Tried several:
- ACES2065-1 (AP0)
- ACEScg (AP1)
- Rec.2020
- DCI-P3\( \)
- Tried several:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Color Space
- Choose another color space?
- Tried several:
- ACES2065-1 (AP0)
- ACEScg (AP1)
- Rec.2020
- DCI-P3
- ACEScg was the best of these, but still bent reds too much towards yellow
- Adjusted red primary x coordinate (0.713 \(\Rightarrow\) 0.75)
- Tried several:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Color Space

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



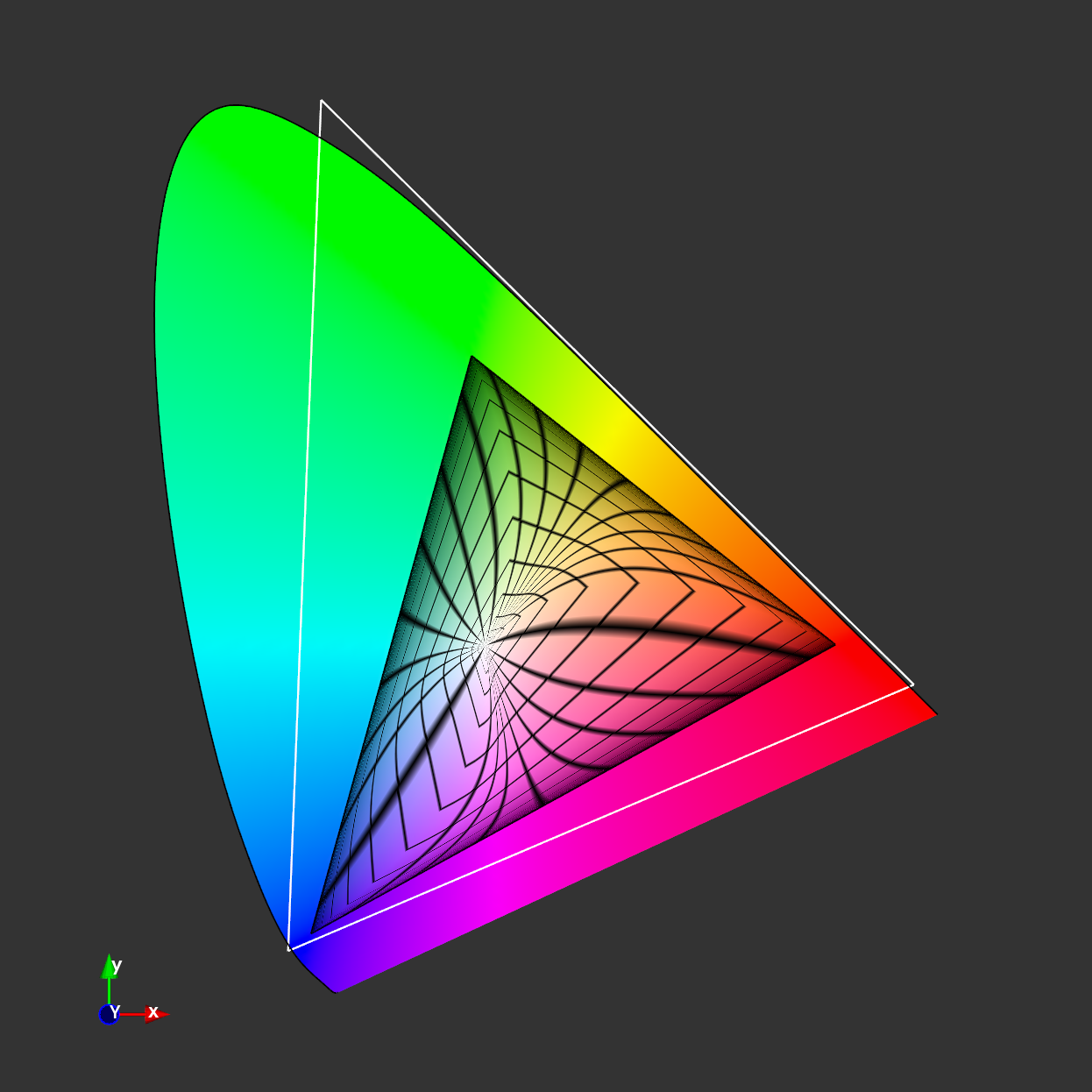
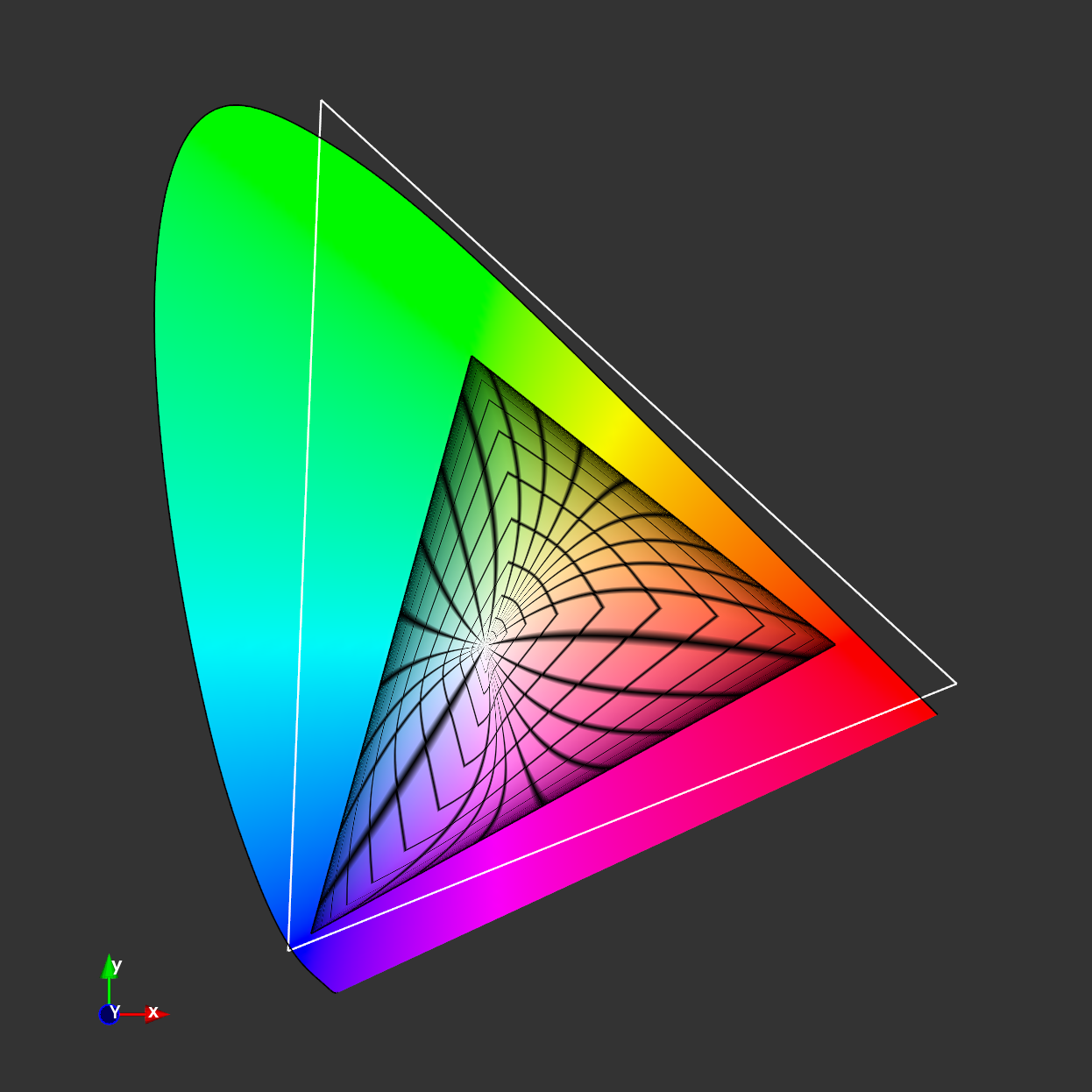
ACEScg
Strong shift of reds towards yellow
Custom
Tonemapping| Color Space

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



ACEScg


Custom Color Space


Tonemapping| White Balance
- Working with old-school grading tools
- Photoshop + 32x32x32 sRGB LUTs
- Still favored by Art Director
- Needed to be conservative to avoid introducing banding
- Too limiting in many cases
- Before tossing our existing pipeline and LUTs, we tried adding white balance controls
- Free, since we can roll it into the Rec.709 \(\Rightarrow\) tonemap matrix
- Worked so well that we didn't need to change our grading approach

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| White Balance
- Artist chose the color they wanted white to change to
- Artists found this more intuitive than typical photographic white balance controls
- Implemented using chromatic adaptation matrix
- Von Kries method using Bradford LMS space
- Does interesting things to the color space!

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| White Balance
- Artist chose the color they wanted white to change to
- Artists found this more intuitive than typical photographic white balance controls
- Implemented using chromatic adaptation matrix
- Von Kries method using Bradford LMS space
- Does interesting things to the color space!

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Without White Balance Adjustment

With Artistic White Balance Adjustment

Tonemapping| Purkinje Shift
- Two challenges when rendering night:
- Make night feel like night, and not just darker day
- Increase visibility in dark areas
- Research has been done in this area
- Dingcai Cao et al., “Rod Contributions to Color Perception: Linear with Rod Contrast”, 2008.
- Adam G. Kirk, “Tone Mapping for Low-Light Conditions”, 2011
- Based on measurements done on the human visual system

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Purkinje Shift
Human Visual System
- Receptors:
- Long, medium, short cones (normal color vision)
- Rods (low-light vision, monochromatic)
- Vision is 3D, not 4D
- Rods use same neural pathways as cones
- Night vision is not “black & white”
- Color shift introduced by rods as they take over \(\Rightarrow\) Purkinje Shift

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Purkinje Shift
- The Purkinje shift can be modeled as a delta in opponent color space
- Color space believed to be used by the visual system
- Need a way to convert between HDR scene colors and cone/rod excitations
- Cone and rod wavelength response curves are available
- So need scene RGB \(\Rightarrow\) spectrum
- Brian Smits, “An RGB to Spectrum Conversion for Reflectances”, 2000

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



RGB Reflectance Spectra \(\mathcal{R}_j\;(j \in \{r, g, b\})\)
Wavelength (nm)
Reflectance
Tonemapping| Purkinje Shift
- Calculate matrix from RGB to LMSR (using D65 illuminant)

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- \(\mathbf{M}\): Matrix to convert from RGB to LMSR
- \(i \in \{L, M, S, R\}\)
- \(j \in \{r, g, b\}\)
- \(\lambda, \Lambda\): Wavelength & range of visible wavelengths
- \(\mathcal{E}_i(\lambda)\): Receptor response curve
- \(\mathcal{I}(\lambda)\): CIE D65 illuminant spectrum (Rec.709 white point)
- \(\mathcal{R}_j(\lambda)\): Rec.709 reflectance spectrum
Tonemapping| Purkinje Shift
- Convert from scene color \(\mathbf{c}\) to LMSR response \(\mathbf{q}\):

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- Calculate multiplicative gain control \(\mathbf{g}\):
- \(i \in \{L, M, S\}\)
- \(\mathbf{m}_i\): maximal cone sensitivity (\(\mathbf{m} = \left[0.63721, 0.39242, 1.6064\right]\))
- \(\mathbf{k}_i\): rod input strength with \(\mathbf{k}_L = \mathbf{k}_M\)
- We used \(\mathbf{k}_L = \mathbf{k}_M = 0.2, \mathbf{k}_S = 0.29\)
Tonemapping| Purkinje Shift
- For a color \(\mathbf{\hat{q}}\) in LMS space, the opponent space color \(\mathbf{o}\) is given by:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Purkinje Shift
- We can now calculate the incremental effect \(\Delta\mathbf{o}\) that the rods have in opponent color space:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- \(K\): Scaling constant (\(K=45.0\))
- \(S\): Static saturation (\(S=10.0\))
- \(k_3\): Surround strength of opponent signal (\(k_3=0.6\))
- \(r_w\): Ratio of responses for white light (\(r_w=0.139\))
- \(p\): Relative weight of L cones (\(p=0.6189\))
Tonemapping| Purkinje Shift
- The RGB color change is then given by:

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



- \(\mathbf{\hat{M}}\): LMS 3x3 submatrix of \(\mathbf{M}\)
- Shader code is straightforward:
float3 PurkineShift(
float3 rgbLightHdr,
float4x3 matLmsrFromRgb,
float3x3 matRgbFromLmsGain)
{
float4 lmsr = mul(matLmsrFromRgb, rgbLightHdr);
float3 lmsGain = rsqrt(1.0f + lmsr.xyz);
return rgbLightHdr + mul(matRgbFromLmsGain, lmsGain) * lmsr.w;
}
Tonemapping| Purkinje Shift

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Tonemapping| Purkinje Shift

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



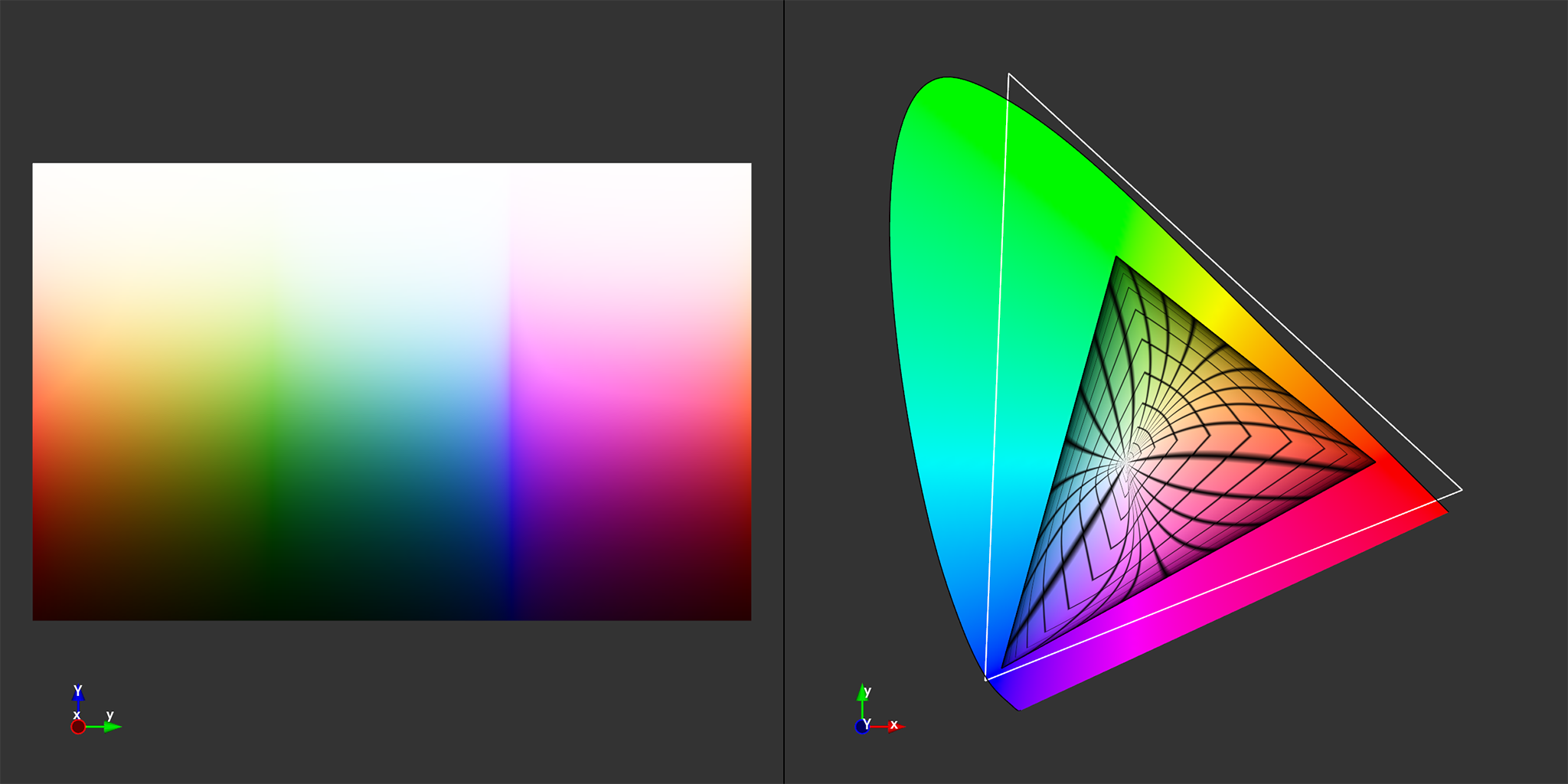
No Purkinje Shift
Tonemapping| Purkinje Shift

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



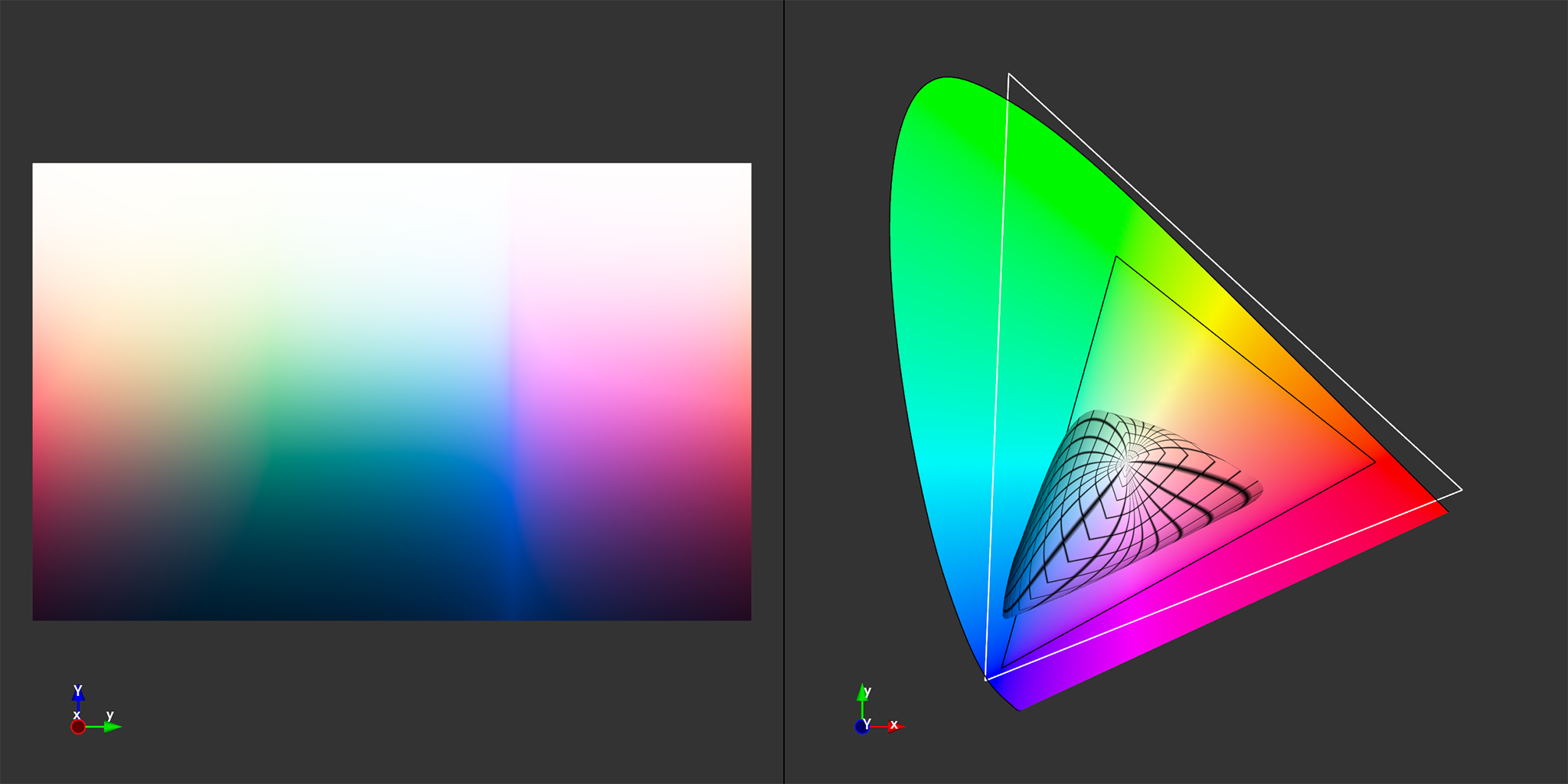
Average Illuminance 0.05 lux
Without Purkinje Shift

With Purkinje Shift

Acknowledgements
- Sucker Punch rendering programmers:
- Adrian Bentley
- Bill Rockenbeck
- Eric Wohllaib
- Matthew Pohlmann
- Tom Low
- The Sucker Punch lighting team: Jeremy Forbes, Rob Simpson, Gaby Soto, and Toby Tobler
- Jason Connell for the many discussions about sky color

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course



Acknowledgements
- Matthijs De Smedt, Dave Elder, and Roman Margold for their contributions to this work
- Joanna Wang for her assistance with assets for this talk
- Everybody at Sucker Punch for making everything awesome
- Natalya Tatarchuk for organizing this course
- My family for their endless patience, support, and love

SIGGRAPH 2021 ADVANCES IN
REAL-TIME RENDERING IN GAMES course




References
- [Ben14] Adrian Bentley. Engine postmortem of inFAMOUS: Second Son. Game Developer’s Conference (video at https://www.gdcvault.com/play/1020399/Engine-Postmortem-of-inFAMOUS-Second and slides at https://www.suckerpunch.com/iss-engine-gdc2014/), 2014.
- [BN08] Eric Bruneton and Fabrice Neyret. Precomputed atmospheric scattering. In Special Issue: Proceedings of the 19th Eurographics Symposium on Rendering 2008, Computer Graphics Forum. Wiley, 2008.
- [CK07] Mark Colbert and Jařosláv Krivanek. GPU-based importance sampling. In Hubert Nguyen, editor, GPU Gems 3, chapter 20. Addison-Wesley Professional, 1st edition, 2007.
- [CPD07] Jiawen Chen, Sylvain Paris, and Frédo Durand. Real-time edge-aware image processing with the bilateral grid. ACM Trans. Graph., 26(3):103–es, July 2007.
- [CPSZ08] D. Cao, J. Pokorny, V. C. Smith, and A. J. Zele. Rod contributions to color perception: linear with rod contrast. Vision Res, 48(26):2586–2592, Nov 2008.
- [Cup12] Robert Cupisz. Light probe interpolation using tetrahedral tessellations. Game Developer’s Conference, 2012.
- [DD02] Frédo Durand and Julie Dorsey. Fast bilateral filtering for the display of high-dynamic-range images. ACM Trans. Graph., 21(3):257–266, July 2002.
- [DFD+15] Haarm-Pieter Duiker, Alexander Forsythe, Scott Dyer, Ray Feeney, Will McCown, Jim Houston, Andy Maltz, and Doug Walker. ACEScg: A common color encoding for visual effects applications. In Proceedings of the 2015 Symposium on Digital Production, DigiPro ’15, page 53, New York, NY, USA, 2015. Association for Computing Machinery.
- [Dro17a] Michal Drobot. Improved culling for tiled and clustered rendering. SIGGRAPH 2017 Advances in Real-Time Rendering in Games Course (slides available at http://advances.realtimerendering.com/s2017/2017_Sig_Improved_Culling_final.pdf), 2017.
- [Dro17b] Michal Drobot. Rendering of Call of Duty: Infinite Warfare. Digital Dragons (slides available at https://research.activision.com/publications/archives/rendering-of-call-of-dutyinfinite-warfare), 2017.
- [Ele09] Oskar Elek. Rendering parametrizable planetary atmospheres with multiple scattering in real-time. https://cgg.mff.cuni.cz/~oskar/projects/CESCG2009/Elek2009.pdf, 2009.



References
- [Hil16] Sébastien Hillaire. Physically based sky, atmosphere and cloud rendering in frostbite. SIGGRAPH 2016 (slides available at https://blog.selfshadow.com/publications/s2016-shading-course/), 2016.
- [KO11] Adam G. Kirk and James F. O’Brien. Perceptually based tone mapping for low-light conditions. In ACM SIGGRAPH 2011 Papers, SIGGRAPH ’11, New York, NY, USA, 2011. Association for Computing Machinery.
- [Lin17] Bruce Lindbloom. Chromatic adaptation. http://www.brucelindbloom.com/index.html?Eqn_ChromAdapt.html, 2017.
- [Nar20] Krzysztof Narkowicz. GPURealTimeBC6H. https://github.com/knarkowicz/GPURealTimeBC6H, 2020.
- [PD09] Sylvain Paris and Frédo Durand. A fast approximation of the bilateral filter using a signal processing approach. Int. J. Comput. Vision, 81(1):24–52, January 2009.
- [RV11] P. Ramachandran and G. Varoquaux. Mayavi: 3D Visualization of Scientific Data. Computing in Science & Engineering, 13(2):40–51, 2011.
- [Sch15] Andrew Schneider. The real-time volumetric cloudscapes of horizon: Zero dawn. SIGGRAPH 2015 (slides available at https://advances.realtimerendering.com/s2015/), 2015.
- [Sch18] Christian Schüler. Followup to atmospheric scattering—part 1: Overview. http://www.thetenthplanet.de/archives/4519, 2018.
- [SH05] Christian Sigg and Markus Hadwiger. Fast third-order texture filtering. In Matt Pharr, editor, GPU Gems 2, chapter 20. Addison-Wesley Professional, 1st edition, 2005.
- [Slo08] Peter-Pike Sloan. Stupid spherical harmonics (SH) tricks. Game Developer’s Conference (also available at https://ppsloan.org/publications/), 2008.
- [Slo17] Peter-Pike Sloan. Deringing spherical harmonics. In SIGGRAPH Asia 2017 Technical Briefs, SA ’17, New York, NY, USA, 2017. Association for Computing Machinery.
- [Smi99] Brian Smits. An RGB-to-spectrum conversion for reflectances. J. Graph. Tools, 4(4):11–22, December 1999.
- [Wro14] Bartlomiej Wronski. Volumetric fog: Unified, compute shader based solution to atmospheric scattering. SIGGRAPH 2014 (slides available at https://bartwronski.com/publications/), 2014.



References
- [Wro15] Bartlomiej Wronski. White balance and physically based rendering pipelines: Part 1 – introduction. https://bartwronski.com/2015/10/14/white-balance-and-physically-based-rendering-pipelines-part-1-introduction/, 2015.
- [Wro16] Bartlomiej Wronski. Localized tonemapping – is global exposure and global tonemapping operator enough for video games? https://bartwronski.com/2016/08/29/localized-tonemapping/, 2016.
- [Yus13] Egor Yusov. Outdoor light scattering sample update. https://software.intel.com/content/www/us/en/develop/blogs/otdoor-light-scattering-sample-update.html, 2013.


Text

Thank You!
Twitter: @jasminpatry
